Foundations of Math

Should more of your learners with disabilities be proficient in math? This course, focused on mathematical content knowledge, allows general and special education teachers to examine mathematical procedures from a conceptual standpoint and increase sense making for learners who struggle with methods reliant on memorization and procedure. Participants will learn how making pedagogical shifts can increase student engagement and improve math achievement for every learner.
Unit 1: Laying the Foundation
Goal:
Understand the connection between mathematical content knowledge for teaching, impacts on learners, and two frameworks for incorporating that knowledge into lessons.
Objectives:
- Understand how the brain learns math.
- Identify characteristics of number sense and how to teach numbers.
- Incorporate two frameworks, the Components of Number Sense Wheel and Prototype for Lesson Construction, in lesson planning.
Unit 2: Quantity and Magnitude
Goal:
Define quantity and magnitude and understand how they are a starting point for understanding math concepts.
Objectives:
- Define quantity and magnitude.
- Understand how quantities and units combine to give meaning and connect concepts
- Identify the benefits and challenges of a number line.
Unit 3: Numeration
Goal:
Understand that being able to name numbers and quantities is important to math understanding.
Objectives:
- Define numeration.
- Understand concepts behind counting
- Understand why being able to quickly recognize quantities (subitizing) is important in math.
- Experience activities that help students develop subitizing skills.
Unit 4: Equality
Goal:
Explore misconceptions about the equal sign and learn how using the concept of equality strengthens overall math understanding.
Objectives:
- Define equality .
- Identify and explain common misunderstandings students have about the equal sign
- Use equality structures to visualize quantities and solve word problems.
- Explore thePrototype for Lesson Construction and Concrete-Representational-Abstract progression in the context of equality in algebra
Unit 5: Base 10
Goal:
Understand how the Base 10 number system supports people in being more efficient math problem solvers.
Objectives:
- Explain the Base 10 system.
- Explore how the base 10 system is fundamental to understanding operations on decimals and whole numbers.
- Use knowledge of the base 10 system to solve math problems.
Unit 6: Form of a Number
Goal:
See numbers flexibly and understand how using various forms of a number aids in math problem solving and understanding.
Objectives:
- Define form of a number.
- Explain why form of a number is important.
- Solve math problems by using various forms of numbers.
- Explain the difference between memorizing math facts and using strategies to solve problems.
Unit 7: Proportional Reasoning
Goal:
Understand proportional reasoning as a concept that can help learners make sense of mathematics into adulthood, and how that is different from a series of procedures that involve cross multiplication.
Objectives:
- Define proportional reasoning.
- Explore non-numeric experiences that help build proportional reasoning skills
- Identify challenges in teaching proportional reasoning and ways to overcome them.
- Compare and contrast different ways of reasoning about proportional relationships
Unit 8: Algebraic Thinking
Goal:
Algebraic thinking involves using what you know to figure out what you don’t know to solve problems. Learn how algebraic thinking supports math learning at all levels including, but not limited to, Algebra class.
Objectives:
- Define algebraic thinking.
- Understand and identify linear relationships.
- Make sense of the equation y = mx + b
- Identify how algebraic topics can be taught using the Prototype for Lesson Construction.
Unit 9: Geometric Thinking
Goal:
Define geometric thinking, and explore how it supports math problem solving in general, and geometry skills and concepts specifically.
Objectives:
- Define geometric thinking.
- Explore Van Hiele’s levels of geometric thinking.
- Apply geometric thinking to solve math problems.
Unit 10: Making Connections Through Language and Discussion
Goal:
Understand why and how to use the Prototype for Lesson Construction for any lesson. Deepen understanding of operations with fractions through the use of the Prototype.
Objectives:
- Experience the Prototype for Lesson Construction in the context of fraction operations.
- Use fraction tiles to make sense of adding and subtracting fractions.
- Use fraction tiles to make sense of multiplying and dividing by fractions.
Unit 11: Assessment and Data
Goal:
Examine assessment tools that provide data on both conceptual understanding and procedural fluency.
Objectives:
- Explore how data and assessment guide instruction.
- Learn about assessment resources and how they might help educators support student learning.
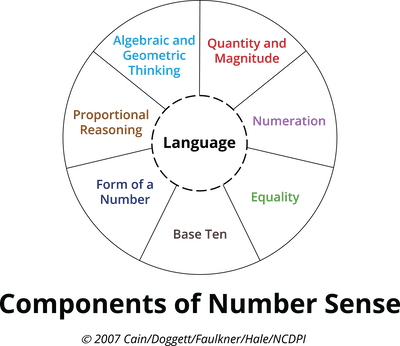
What are the Components of Number Sense?
Reading is not reading if all of the components of reading are not working together (such as fluency, comprehension, vocabulary, phonemic awareness, and phonics). Math is not math if learners are not engaging in, and making connections between, multiple components of number sense.
The phrase “Number Sense” is commonly used, and means different things to different people.
In this training, number sense refers to the integration of the 8 components presented in the Components of Number Sense “wheel,” each component connected to every other component through language. During the training, each component is defined, and participants learn classroom applications, diagnosis questions, and research related to the component.
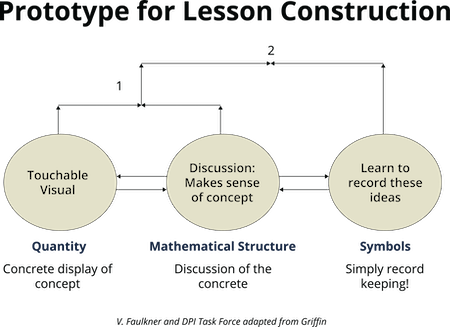
What is the Prototype for Lesson Construction?
Math in the course is taught using the Prototype for Lesson Construction. Participants see it modeled, work through it themselves, and have time to adapt their own lessons to fit this framework.
The prototype is based in developmental and cognitive research about how the brain learns math.
Arrows in the diagram show the need to first build relationships between quantities and language. Second, learners extend that knowledge to understand relationships between quantities, vocabulary, and discourse. Two way arrows between the ovals indicate the need to be fluent between representations, and move among and between quantity, structure, language, and symbols.
Is This for All Disabilities?
The Foundations of Math practices can be applied to teach all students in all settings and implemented with any math curriculum or set of materials.
Both the in-person course and online modules develop mathematical content knowledge and equip teachers to plan math lessons that build conceptual understanding and procedural fluency. Participants will benefit from examples and practice opportunities.
The in-person course provides examples and practice during the course. Online participants are encouraged to seek those opportunities independently in their classrooms, and collaboratively with ancillary staff. Alt+Shift is available to answer questions through their technical assistance form.
Explore the Practice Profile
This practice profile outlines the key components of successful implementation of the information in this course. It highlights evidence-based practices and describes the essential activities that support each component. Practice profiles help teams and individuals assess their current practices, identify areas for growth, and set goals. They can improve consistency among educators, track progress, and guide system improvements.
Why Try Something New?
Learners of all ages should receive a cohesive and coherent mathematics education that allows them to make sense of their world, interact in it, and contribute to it.
Mathematics is often taught procedurally, focusing on memorization and using steps to solve problems. This approach can confuse learners, particularly those with disabilities. Memorizing and keeping track of when to apply certain procedures (and when not to) is difficult.
With greater mathematical content knowledge, educators can reduce efforts aimed at making learners better memorizers and step followers and increase robust mathematical instruction. This will allow learners to make connections between math content and apply knowledge to new math topics and real life situations.
Evidence Base
- Mathematics in the 21st Century: What Mathematical Knowledge is Needed for Teaching Mathematics (Remarks made by Deborah L. Ball at the Secretary's Summit on Mathematics at the U.S. Department of Education in 2003.)
- Teaching Number Sense
- The Learning Trajectories
If you are interested in learning more, check out our full Foundations of Math video series on our YouTube channel.
