Utilizing Games and Activities to Strengthen Number Sense
Description
People who struggle with math may not have had opportunities to develop a strong sense of number. Working with different components of number sense, and making connections between them, helps learners improve number sense and overall problem-solving skills.
Why Try Something New?
There are many formats for math instruction and practice activities. Examples include: computer-based lessons and practice problems, traditional and non-traditional pencil/paper worksheets, flashcards, and fillable note pages.
These activities may work for some learners. If you find they do not work for all learners, consider using games and conceptual activities.
Games and activities can address the same math objectives as the other formats. They can also attend to learning needs such as
- interaction with people
- using math in context
- using language to process thinking
- using visuals to enhance understanding
- providing repetition with variety
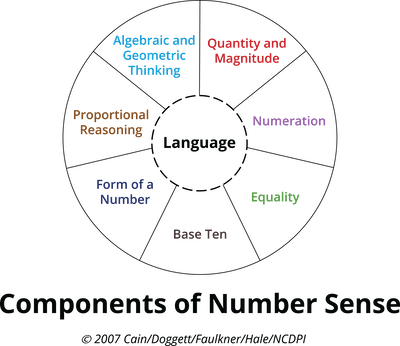
Components of Number Sense
The Components of Number Sense wheel was designed to help educators see the big ideas of math. Using them as building blocks of math lessons provides more meaningful opportunities to develop number sense and conceptual understanding.
The components are defined individually to help readers understand and highlight each component. However, keep in mind that they are not meant to be taught in isolation. Making connections between multiple components within one lesson or activity is what creates a more robust learning opportunity for the students.
The Components of Number Sense include:
- Quantity and Magnitude
- Numeration
- Equality
- Base Ten
- Form of a Number
- Proportional Reasoning
- Algebraic and Geometric Thinking
Language sits in the middle of the wheel. Meaningful discourse about mathematics is what helps learners make connections among the components.
Strengthening Understanding of Quantity and Magnitude
Quantity means how many or how much of something there is.
Magnitude means the size of something as it compares to something else. For example, 3 is a small amount if it is pennies at the grocery store, but a large amount if it is squirrels in your kitchen.
Some ways to build an understanding of quantity and magnitude include:
- Counting objects
- Count by ones with early learners
- Count sets of 2, 3, 5, 10, etc.
- Ask “How many?” so the learner understands why he/she is counting.
- Use counting language with secondary learners to connect their understanding of quantity with new abstract concepts. For example: How many x’s do we have with 5x? How many radical twos do we have altogether 32- 2? How many i’s is 2i + 3i?
- Comparing quantities and magnitudes
- More/Less
- Shorter/Longer
- Bigger/Smaller
- Recognizing quantities
- 2 tires on a bike; 4 chairs at a table
- 6 petals on a flower, how many petals on 4 flowers?
- 3 lengths of a diameter around a circle
- Matching quantities shown with different objects
- 3 blocks and 3 crayons
- 7 crackers and 7 dots
- 3 sets of 4 crackers and 2 sets of 6 chips
- 3 scoops of ⅔ of a cup and ⅔ of a set of 3
To emphasize quantity and magnitude, focus on the connection between the amounts of objects and how they compare to other amounts.
The activities listed below are examples of games and activities to help learners develop quantity and magnitude.
Printable Activities:
Egg Carton Skip Counting (1-4)
Several Skip Counting Activities (K-5) [PDF]
Virtual Activities:
Strengthening Understanding of Numeration
Numeration means naming a given quantity or calculation.
Numbers (the actual amount of something) can be written as words, as numerals with digits, and spoken verbally. All forms of numeration are important to explain and share with learners.
To develop numeration:
- Start with the quantity and spoken language to name it. For early math learners, this starts with the counting numbers. For higher level math, this includes other kinds of numbers (for example, fractions, integers, and irrational numbers).
- As the learner develops understanding of the quantity and its name(s), introduce the digit(s) or symbolic representation for the quantity and language.
To emphasize numeration, focus on the connection between the names of the amounts and the actual amounts.
The activities listed below can be used to help learners develop numeration.
Printable Activities
Learning Trajectories-Subitizing (K-3)
Virtual Activities
Splash Learn - Use Base 10 Blocks to Make a Number (Grade 2)
Strengthening Understanding of Equality
Equality means having the same value.
Some ways to build an understanding of equality include:
- Counting sets of different objects (e.g., blocks and crayons) to see if they are equal or unequal amounts
- Looking at different ways to separate sets of objects that show the same amount
- 5 red blocks is equal to 3 blue blocks and 2 yellow blocks
- 4 cups of 6 crackers is equal to 2 cups of 12 crackers
- Working with different measurements that show equal amounts
- a half cup of water equals two quarter cups
- 12 one-inch strips of yarn is equal to one foot of yarn
To emphasize equality, focus on the connection between how two or more amounts show the same value.
The activities listed below can be used to help learners develop equality.
Printable Activities
Virtual Activities
Strengthening Understanding of Base Ten
Base Ten is the name of the number system we use. It is called base ten because it uses ten digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) to show any value.
We can count up to 9 things and when we get a 10th item, we bundle them together to make a “ten” and start again at 0. That’s why 10 ones makes a ten, 10 tens make one hundred, and so on.
Some ways to build an understanding of base ten includes:
- Count objects and group them into sets of ten.
- Use ten frames to develop the understanding of filling a base of ten.
- Explore different values using base ten blocks (blocks that show single units, units of ten, and units of a hundred)
- Write numbers in digit form using a place value mat.
- Explore expanded form
- Did you know that other number systems exist? Explore other bases to deepen the understanding of a base number system.
To emphasize base ten, focus on making/composing groups of ten.
- Early learners will focus on quantities to 10.
- Intermediate learners will add understanding of powers of 10. Powers of 10 happen when we multiply or divide by 10. Place value, large numbers, and decimals are examples of this.
The activities listed below can be used to help learners develop an understanding of base ten.
Virtual Activities
Strengthening Form of a Number
Form of a number means numbers can be written in different ways (for example, 25 can also be written as 20 + 5; 15 + 10; 30 – 5; 5 x 5; 100 ÷ 4; etc.).
Being able to write numbers in different ways can make problem-solving easier because the learner can use numbers that are easier to work with or numbers that they understand better.
Some ways to build an understanding of form of a number include:
- Put a set number of beads on a string and leave enough room to move the beads along the string. Separate the beads in different ways and record the ideas. For example:
- 10 can be 2 beads and 8 beads, or 6 beads and 4 beads
- 12 can be 6 beads and 6 beads, or 9 beads and 3 beads
- Choose a number and think of all the ways you can break the number down into smaller parts and still have the amount you started with. For example:
- 18 = 9 + 9; 18 = 10 + 5 + 3
- 25 = 20 + 5; 18 + 7; 30 - 5; 5 x 5
- Work with money to create different ways to pay for something using different bills and/or coins.
- Brainstorm ways to write fractions or mixed numbers in different ways.
- Explore the conversion of fractions to decimals and record them on a number line.
To emphasize form of a number, focus on the ability to show the same quantities in different ways.
The activities listed below can be used to help learners develop an understanding of form of a number.
Printable Activities
Virtual Activities
Strengthening Proportional Reasoning
Proportional reasoning is the ability to see a relationship between two quantities using multiplication.
There are many ways to see relationships between quantities. The key to proportional reasoning is that the relationship involves multiplication (and not addition).
Example: For every apple tree, I picked 2 apples.
- In this case, the two quantities are the number of trees and the number of apples.
- The proportional relationship is “times 2” or “multiply by 2” because I can multiply the number of trees by 2 to figure out how many apples I picked.
Non-example: I picked two apples off of each tree.
- I have 2 apples, plus 2 apples, plus 2 apples, and on and on.
- In this non-example, the relationship is “plus 2” because we are adding 2 each time. We are not multiplying.
Proportional reasoning is critical because learners will encounter many relationships that involve multiplication in real-life problems and advanced math courses.
Some ways to build an understanding of proportional reasoning include:
- Play a copycat game using proportions. For every one jumping jack I do, you have to do three.
- Build with blocks and set a rate such as for every two red blocks I use, I have to use three blue blocks. How many blue blocks will I use if I have 3 red?
- Create art pieces on grid paper with proportions. For example, for every square I color yellow, I have to color 5 squares purple. How many purple squares will I need with 3 yellow?
- Make a scale drawing of your room with a proportion (for example, every inch in my drawing will represent 12 inches in my room).
To emphasize proportional reasoning, focus on the relationship between numbers using multiplication.
The activities listed below can be used to help learners develop proportional reasoning.
Printable Activities
Egg Carton Skip Counting (1-4)
Virtual Activities
Strengthening Algebraic and Geometric Thinking
Algebraic thinking includes recognizing patterns and using numerical relationships to understand real-world scenarios and how things change.
Geometric thinking involves understanding the size, shape, position, and dimensions of things.
Some ways to strengthen algebraic and geometric thinking include:
- Finding shapes in a picture hunt
- Create patterns with different objects
- Sorting figures into categories (number of sides, number of points, straight/curved lines, interior angle measures, etc.)
- Play with tangrams and create figures using different shapes
- Creating graphs and charts and discussing the patterns and relationships they show using numerical values from real-world scenarios
- Figuring out unknown quantities like “There are 8 eggs in a carton that holds 12 eggs, how many eggs were taken out?”
To emphasize algebraic and geometric thinking, focus on the patterns and spatial relationships that help to explain what happens in the real world.
The activities listed below can be used to help learners develop algebraic and geometric thinking.
Printable Activities
Virtual Activities
What’s Going on in this Graph? (7-12)
Prodigy: Mobius Strip (Scroll down to #7 in the list)
Multi-Format K-8 Operations & Algebraic Thinking Resources
Resources available in multiple formats for educators to access by specific grades and content topics.
PBS Learning Media: K-8 Mathematics, Operations and Algebraic Thinking (K-8)
